Résolveur d'équations du second degré

L'équation est de la forme : ax2+bx+c=0, et il faut trouver s'il y a des valeurs pour x telles que cette équation se vérifie. Pour cela, on calcule le discriminant delta noté d=b2-4.a.c.

Valeur de d
 Solutions de l'équation
Calcul des solutions
>0
deux solutions réelles distinctes
X indice 1 égal à numérateur de la fraction moins b moins racine carrée de d au-dessus du dénominateur 2. a fin de la fraction espace e t espace X indice 2 égal à numérateur de la fraction moins b plus racine carrée de d au-dessus du dénominateur 2. a fin de la fraction
0
une solution réelle double
X indice 1 égal à numérateur de la fraction moins b au-dessus du dénominateur 2. a fin de la fraction
<0
deux solutions complexes distinctes

 

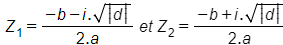Voici un résolveur pour la ou les solutions réelles. Entrez les valeurs de a, b et c (chacun<10000) :

Coefficients : x2+ x+ =0    

Solutions :    x1 =
  x2 =
Modifié le: mercredi 29 novembre 2023, 22:24